Statistics¶
This chapter describes the statistical functions in the library. The basic statistical functions include routines to compute the mean, variance and standard deviation. More advanced functions allow you to calculate absolute deviations, skewness, and kurtosis as well as the median and arbitrary percentiles. The algorithms use recurrence relations to compute average quantities in a stable way, without large intermediate values that might overflow.
Data Types¶
The functions are available in versions for datasets in the standard
floating-point and integer types. The versions for double precision
floating-point data have the prefix cml_stats and are declared in
the header file cml/statistics/double.h. The versions for integer
data have the prefix cml_stats_int and are declared in the header
file cml/statistics/int.h. All the functions operate on C
arrays with a stride parameter specifying the spacing between
elements. The full list of available types is given below,
| Prefix | Type |
|---|---|
| cml_stats | double |
| cml_stats_float | float |
| cml_stats_long_double | long double |
| cml_stats_int | int |
| cml_stats_uint | unsigned int |
| cml_stats_long | long |
| cml_stats_ulong | unsigned long |
| cml_stats_short | short |
| cml_stats_ushort | unsigned short |
| cml_stats_char | char |
| cml_stats_uchar | unsigned char |
| cml_stats_complex | complex double |
| cml_stats_complex_float | complex float |
| cml_stats_complex_long_double | complex long double |
Mean, Standard Deviation and Variance¶
-
double
cml_stats_mean(const double data[], size_t stride, size_t n)¶ This function returns the arithmetic mean of
data, a dataset of lengthnwith stridestride. The arithmetic mean, or sample mean, is denoted by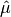 and defined as,
and defined as,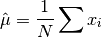
where
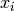 are the elements of the dataset
are the elements of the dataset data. For samples drawn from a gaussian distribution the variance of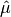 is
is 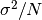 .
.
-
double
cml_stats_variance(const double data[], size_t stride, size_t n)¶ This function returns the estimated, or sample, variance of
data, a dataset of lengthnwith stridestride. The estimated variance is denoted by and is defined by,
and is defined by,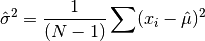
where
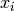 are the elements of the dataset
are the elements of the dataset data. Note that the normalization factor of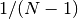 results from the derivation
of
results from the derivation
of  as an unbiased estimator of the population
variance
as an unbiased estimator of the population
variance 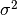 . For samples drawn from a Gaussian distribution
the variance of
. For samples drawn from a Gaussian distribution
the variance of  itself is
itself is 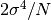 .
.This function computes the mean via a call to
cml_stats_mean(). If you have already computed the mean then you can pass it directly tocml_stats_variance_m().
-
double
cml_stats_variance_m(const double data[], size_t stride, size_t n, double mean)¶ This function returns the sample variance of
datarelative to the given value ofmean. The function is computed with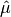 replaced by the value of
replaced by the value of meanthat you supply,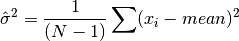
-
double
cml_stats_sd(const double data[], size_t stride, size_t n)¶ -
double
cml_stats_sd_m(const double data[], size_t stride, size_t n, double mean)¶ The standard deviation is defined as the square root of the variance. These functions return the square root of the corresponding variance functions above.
-
double
cml_stats_tss(const double data[], size_t stride, size_t n)¶ -
double
cml_stats_tss_m(const double data[], size_t stride, size_t n, double mean)¶ These functions return the total sum of squares (TSS) of
dataabout the mean. Forcml_stats_tss_m()the user-supplied value ofmeanis used, and forcml_stats_tss()it is computed usingcml_stats_mean().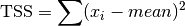
-
double
cml_stats_variance_with_fixed_mean(const double data[], size_t stride, size_t n, double mean)¶ This function computes an unbiased estimate of the variance of
datawhen the population meanmeanof the underlying distribution is known a priori. In this case the estimator for the variance uses the factor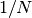 and the sample mean
and the sample mean
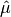 is replaced by the known population mean
is replaced by the known population mean 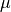 ,
,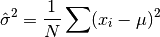
-
double
cml_stats_sd_with_fixed_mean(const double data[], size_t stride, size_t n, double mean)¶ This function calculates the standard deviation of
datafor a fixed population meanmean. The result is the square root of the corresponding variance function.
Absolute deviation¶
-
double
cml_stats_absdev(const double data[], size_t stride, size_t n)¶ This function computes the absolute deviation from the mean of
data, a dataset of lengthnwith stridestride. The absolute deviation from the mean is defined as,
where
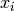 are the elements of the dataset
are the elements of the dataset data. The absolute deviation from the mean provides a more robust measure of the width of a distribution than the variance. This function computes the mean ofdatavia a call tocml_stats_mean().
-
double
cml_stats_absdev_m(const double data[], size_t stride, size_t n, double mean)¶ This function computes the absolute deviation of the dataset
datarelative to the given value ofmean,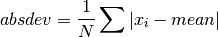
This function is useful if you have already computed the mean of
data(and want to avoid recomputing it), or wish to calculate the absolute deviation relative to another value (such as zero, or the median).
Higher moments (skewness and kurtosis)¶
-
double
cml_stats_skew(const double data[], size_t stride, size_t n)¶ This function computes the skewness of
data, a dataset of lengthnwith stridestride. The skewness is defined as,
where
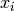 are the elements of the dataset
are the elements of the dataset data. The skewness measures the asymmetry of the tails of a distribution.The function computes the mean and estimated standard deviation of
datavia calls tocml_stats_mean()andcml_stats_sd().
-
double
cml_stats_skew_m_sd(const double data[], size_t stride, size_t n, double mean, double sd)¶ This function computes the skewness of the dataset
datausing the given values of the meanmeanand standard deviationsd,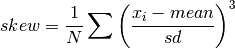
These functions are useful if you have already computed the mean and standard deviation of
dataand want to avoid recomputing them.
-
double
cml_stats_kurtosis(const double data[], size_t stride, size_t n)¶ This function computes the kurtosis of
data, a dataset of lengthnwith stridestride. The kurtosis is defined as,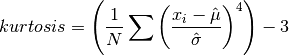
The kurtosis measures how sharply peaked a distribution is, relative to its width. The kurtosis is normalized to zero for a Gaussian distribution.
-
double
cml_stats_kurtosis_m_sd(const double data[], size_t stride, size_t n, double mean, double sd)¶ This function computes the kurtosis of the dataset
datausing the given values of the meanmeanand standard deviationsd,
This function is useful if you have already computed the mean and standard deviation of
dataand want to avoid recomputing them.
Autocorrelation¶
-
double
cml_stats_lag1_autocorrelation(const double data[], const size_t stride, const size_t n)¶ This function computes the lag-1 autocorrelation of the dataset
data.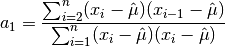
-
double
cml_stats_lag1_autocorrelation_m(const double data[], const size_t stride, const size_t n, const double mean)¶ This function computes the lag-1 autocorrelation of the dataset
datausing the given value of the meanmean.
Covariance¶
-
double
cml_stats_covariance(const double data1[], const size_t stride1, const double data2[], const size_t stride2, const size_t n)¶ This function computes the covariance of the datasets
data1anddata2which must both be of the same lengthn.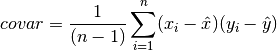
-
double
cml_stats_covariance_m(const double data1[], const size_t stride1, const double data2[], const size_t stride2, const size_t n, const double mean1, const double mean2)¶ This function computes the covariance of the datasets
data1anddata2using the given values of the means,mean1andmean2. This is useful if you have already computed the means ofdata1anddata2and want to avoid recomputing them.
Correlation¶
-
double
cml_stats_correlation(const double data1[], const size_t stride1, const double data2[], const size_t stride2, const size_t n)¶ This function efficiently computes the Pearson correlation coefficient between the datasets
data1anddata2which must both be of the same lengthn.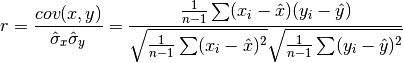
-
double
cml_stats_spearman(const double data1[], const size_t stride1, const double data2[], const size_t stride2, const size_t n, double work[])¶ This function computes the Spearman rank correlation coefficient between the datasets
data1anddata2which must both be of the same lengthn. Additional workspace of size 2 *nis required inwork. The Spearman rank correlation between vectors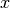 and
and
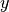 is equivalent to the Pearson correlation between the ranked
vectors
is equivalent to the Pearson correlation between the ranked
vectors 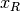 and
and 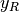 , where ranks are defined to be the
average of the positions of an element in the ascending order of the values.
, where ranks are defined to be the
average of the positions of an element in the ascending order of the values.
Maximum and Minimum values¶
The following functions find the maximum and minimum values of a
dataset (or their indices). If the data contains NaN-s then a
NaN will be returned, since the maximum or minimum value is
undefined. For functions which return an index, the location of the
first NaN in the array is returned.
-
double
cml_stats_max(const double data[], size_t stride, size_t n)¶ This function returns the maximum value in
data, a dataset of lengthnwith stridestride. The maximum value is defined as the value of the element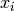 which satisfies
which satisfies 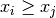 for all
for all  .
.If you want instead to find the element with the largest absolute magnitude you will need to apply
fabs()orabs()to your data before calling this function.
-
double
cml_stats_min(const double data[], size_t stride, size_t n)¶ This function returns the minimum value in
data, a dataset of lengthnwith stridestride. The minimum value is defined as the value of the element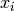 which satisfies
which satisfies 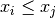 for all
for all  .
.If you want instead to find the element with the smallest absolute magnitude you will need to apply
fabs()orabs()to your data before calling this function.
-
void
cml_stats_minmax(double * min, double * max, const double data[], size_t stride, size_t n)¶ This function finds both the minimum and maximum values
min,maxindatain a single pass.
-
size_t
cml_stats_max_index(const double data[], size_t stride, size_t n)¶ This function returns the index of the maximum value in
data, a dataset of lengthnwith stridestride. The maximum value is defined as the value of the element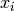 which satisfies
which satisfies
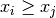 for all
for all  . When there are several equal maximum
elements then the first one is chosen.
. When there are several equal maximum
elements then the first one is chosen.
-
size_t
cml_stats_min_index(const double data[], size_t stride, size_t n)¶ This function returns the index of the minimum value in
data, a dataset of lengthnwith stridestride. The minimum value is defined as the value of the element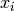 which satisfies
which satisfies
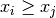 for all
for all  . When there are several equal
minimum elements then the first one is chosen.
. When there are several equal
minimum elements then the first one is chosen.
-
void
cml_stats_minmax_index(size_t * min_index, size_t * max_index, const double data[], size_t stride, size_t n)¶ This function returns the indexes
min_index,max_indexof the minimum and maximum values indatain a single pass.
Median and Percentiles¶
The median and percentile functions described in this section operate on sorted data. For convenience we use quantiles, measured on a scale of 0 to 1, instead of percentiles (which use a scale of 0 to 100).
-
double
cml_stats_median_from_sorted_data(const double sorted_data[], size_t stride, size_t n)¶ This function returns the median value of
sorted_data, a dataset of lengthnwith stridestride. The elements of the array must be in ascending numerical order. There are no checks to see whether the data are sorted, so the functioncml_sort()should always be used first.When the dataset has an odd number of elements the median is the value of element
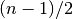 . When the dataset has an even number of
elements the median is the mean of the two nearest middle values,
elements
. When the dataset has an even number of
elements the median is the mean of the two nearest middle values,
elements 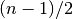 and
and 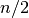 . Since the algorithm for
computing the median involves interpolation this function always returns
a floating-point number, even for integer data types.
. Since the algorithm for
computing the median involves interpolation this function always returns
a floating-point number, even for integer data types.
-
double
cml_stats_quantile_from_sorted_data(const double sorted_data[], size_t stride, size_t n, double f)¶ This function returns a quantile value of
sorted_data, a double-precision array of lengthnwith stridestride. The elements of the array must be in ascending numerical order. The quantile is determined by thef, a fraction between 0 and 1. For example, to compute the value of the 75th percentilefshould have the value 0.75.There are no checks to see whether the data are sorted, so the function
cml_sort()should always be used first.The quantile is found by interpolation, using the formula
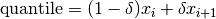
where
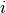 is
is floor((n - 1)f)and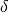 is
is
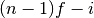 .
.Thus the minimum value of the array (
data[0*stride]) is given byfequal to zero, the maximum value (data[(n-1)*stride]) is given byfequal to one and the median value is given byfequal to 0.5. Since the algorithm for computing quantiles involves interpolation this function always returns a floating-point number, even for integer data types.
References and Further Reading¶
The standard reference for almost any topic in statistics is the multi-volume Advanced Theory of Statistics by Kendall and Stuart.
- Maurice Kendall, Alan Stuart, and J. Keith Ord. The Advanced Theory of Statistics (multiple volumes) reprinted as Kendall’s Advanced Theory of Statistics. Wiley, ISBN 047023380X.
Many statistical concepts can be more easily understood by a Bayesian approach. The following book by Gelman, Carlin, Stern and Rubin gives a comprehensive coverage of the subject.
- Andrew Gelman, John B. Carlin, Hal S. Stern, Donald B. Rubin. Bayesian Data Analysis. Chapman & Hall, ISBN 0412039915.