Numerical Differentiation¶
The functions described in this chapter compute numerical derivatives by finite differencing. An adaptive algorithm is used to find the best choice of finite difference and to estimate the error in the derivative.
The functions described in this chapter are declared in the header
file cml/deriv.h.
Functions¶
-
int
cml_deriv_central(const cml_function_t *f, double x, double h, double *result, double *abserr)¶ This function computes the numerical derivative of the function
fat the pointxusing an adaptive central difference algorithm with a step-size ofh. The derivative is returned inresultand an estimate of its absolute error is returned inabserr.The initial value of
his used to estimate an optimal step-size, based on the scaling of the truncation error and round-off error in the derivative calculation. The derivative is computed using a 5-point rule for equally spaced abscissae at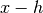 ,
, 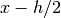 ,
, 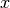 ,
,
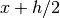 ,
, 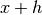 , with an error estimate taken from the difference
between the 5-point rule and the corresponding 3-point rule
, with an error estimate taken from the difference
between the 5-point rule and the corresponding 3-point rule 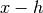 ,
,
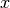 ,
, 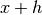 . Note that the value of the function at
. Note that the value of the function at 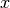 does not contribute to the derivative calculation, so only 4-points are
actually used.
does not contribute to the derivative calculation, so only 4-points are
actually used.
-
int
cml_deriv_forward(const cml_function_t *f, double x, double h, double *result, double *abserr)¶ This function computes the numerical derivative of the function
fat the pointxusing an adaptive forward difference algorithm with a step-size ofh. The function is evaluated only at points greater thanx, and never atxitself. The derivative is returned inresultand an estimate of its absolute error is returned inabserr. This function should be used if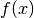 has a
discontinuity at
has a
discontinuity at x, or is undefined for values less thanx.The initial value of
his used to estimate an optimal step-size, based on the scaling of the truncation error and round-off error in the derivative calculation. The derivative at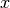 is computed using an
“open” 4-point rule for equally spaced abscissae at
is computed using an
“open” 4-point rule for equally spaced abscissae at 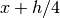 ,
,
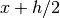 ,
, 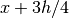 ,
, 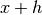 , with an error estimate taken
from the difference between the 4-point rule and the corresponding
2-point rule
, with an error estimate taken
from the difference between the 4-point rule and the corresponding
2-point rule 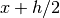 ,
, 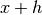 .
.
-
int
cml_deriv_backward(const cml_function_t *f, double x, double h, double *result, double *abserr)¶ This function computes the numerical derivative of the function
fat the pointxusing an adaptive backward difference algorithm with a step-size ofh. The function is evaluated only at points less thanx, and never atxitself. The derivative is returned inresultand an estimate of its absolute error is returned inabserr. This function should be used if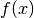 has a discontinuity at
has a discontinuity at x, or is undefined for values greater thanx.This function is equivalent to calling
cml_deriv_forward()with a negative step-size.
Examples¶
The following code estimates the derivative of the function
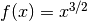 at
at 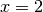 and at
and at 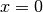 . The function
. The function 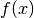 is
undefined for
is
undefined for  so the derivative at
so the derivative at 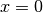 is computed
using
is computed
using cml_deriv_forward().
#include <stdio.h>
#include <cml.h>
double
f(double x, void *params)
{
(void)(params); /* avoid unused parameter warning */
return pow(x, 1.5);
}
int
main(void)
{
cml_function_t F;
double result, abserr;
F.function = &f;
F.params = 0;
printf("f(x) = x^(3/2)\n");
cml_deriv_central(&F, 2.0, 1e-8, &result, &abserr);
printf("x = 2.0\n");
printf("f'(x) = %.10f +/- %.10f\n", result, abserr);
printf("exact = %.10f\n\n", 1.5 * sqrt(2.0));
cml_deriv_forward (&F, 0.0, 1e-8, &result, &abserr);
printf("x = 0.0\n");
printf("f'(x) = %.10f +/- %.10f\n", result, abserr);
printf("exact = %.10f\n", 0.0);
return 0;
}
Here is the output of the program,
f(x) = x^(3/2)
x = 2.0
f'(x) = 2.1213203120 +/- 0.0000005006
exact = 2.1213203436
x = 0.0
f'(x) = 0.0000000160 +/- 0.0000000339
exact = 0.0000000000
References and Further Reading¶
The algorithms used by these functions are described in the following sources:
- Abramowitz and Stegun, Handbook of Mathematical Functions, Section 25.3.4, and Table 25.5 (Coefficients for Differentiation).
- S.D. Conte and Carl de Boor, Elementary Numerical Analysis: An Algorithmic Approach, McGraw-Hill, 1972.