IEEE floating-point arithmetic¶
This chapter describes functions for examining the representation of
floating point numbers and controlling the floating point environment of
your program. The functions described in this chapter are declared in
the header file cml/ieee.h.
Representation of floating point numbers¶
The IEEE Standard for Binary Floating-Point Arithmetic defines binary
formats for single and double precision numbers. Each number is composed
of three parts: a sign bit ( ), an exponent
(
), an exponent
(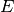 ) and a fraction (
) and a fraction (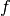 ). The numerical value of the
combination
). The numerical value of the
combination 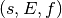 is given by the following formula,
is given by the following formula,
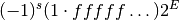
The sign bit is either zero or one. The exponent ranges from a minimum value
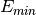 to a maximum value
to a maximum value
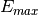 depending on the precision. The exponent is converted to an
unsigned number
depending on the precision. The exponent is converted to an
unsigned number
 , known as the biased exponent, for storage by adding a
bias parameter,
, known as the biased exponent, for storage by adding a
bias parameter,
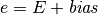
The sequence 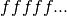 represents the digits of the binary
fraction
represents the digits of the binary
fraction 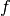 . The binary digits are stored in normalized
form, by adjusting the exponent to give a leading digit of
. The binary digits are stored in normalized
form, by adjusting the exponent to give a leading digit of 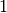 .
Since the leading digit is always 1 for normalized numbers it is
assumed implicitly and does not have to be stored.
Numbers smaller than
.
Since the leading digit is always 1 for normalized numbers it is
assumed implicitly and does not have to be stored.
Numbers smaller than
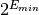 are be stored in denormalized form with a leading zero,
are be stored in denormalized form with a leading zero,

This allows gradual underflow down to
 for
for 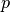 bits of precision.
A zero is encoded with the special exponent of
bits of precision.
A zero is encoded with the special exponent of
 and infinities with the exponent of
and infinities with the exponent of
 .
.
The format for single precision numbers uses 32 bits divided in the following way:
seeeeeeeefffffffffffffffffffffff
s = sign bit, 1 bit
e = exponent, 8 bits (E_min=-126, E_max=127, bias=127)
f = fraction, 23 bits
The format for double precision numbers uses 64 bits divided in the following way:
seeeeeeeeeeeffffffffffffffffffffffffffffffffffffffffffffffffffff
s = sign bit, 1 bit
e = exponent, 11 bits (E_min=-1022, E_max=1023, bias=1023)
f = fraction, 52 bits
It is often useful to be able to investigate the behavior of a calculation at the bit-level and the library provides functions for printing the IEEE representations in a human-readable form.
-
void
cml_ieee754_fprintf_float(FILE * stream, const float * x)¶ -
void
cml_ieee754_fprintf_double(FILE * stream, const double * x)¶ These functions output a formatted version of the IEEE floating-point number pointed to by
xto the streamstream. A pointer is used to pass the number indirectly, to avoid any undesired promotion fromfloattodouble. The output takes one of the following forms,NaNthe Not-a-Number symbolInf, -Infpositive or negative infinity1.fffff...*2^E, -1.fffff...*2^Ea normalized floating point number0.fffff...*2^E, -0.fffff...*2^Ea denormalized floating point number0, -0positive or negative zeroThe output can be used directly in GNU Emacs Calc mode by preceding it with
2#to indicate binary.
-
void
cml_ieee754_printf_float(const float * x)¶ -
void
cml_ieee754_printf_double(const double * x)¶ These functions output a formatted version of the IEEE floating-point number pointed to by
xto the streamstdout.
The following program demonstrates the use of the functions by printing
the single and double precision representations of the fraction
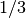 . For comparison the representation of the value promoted from
single to double precision is also printed.
. For comparison the representation of the value promoted from
single to double precision is also printed.
#include <stdio.h>
#include <cml.h>
int
main(void)
{
float f = 1.0/3.0;
double d = 1.0/3.0;
double fd = f; /* promote from float to double */
printf(" f = ");
cml_ieee754_printf_float(&f);
printf("\n");
printf("fd = ");
cml_ieee754_printf_double(&fd);
printf("\n");
printf(" d = ");
cml_ieee754_printf_double(&d);
printf("\n");
return 0;
}
The binary representation of 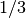 is
is  . The
output below shows that the IEEE format normalizes this fraction to give
a leading digit of 1:
. The
output below shows that the IEEE format normalizes this fraction to give
a leading digit of 1:
f = 1.01010101010101010101011*2^-2
fd = 1.0101010101010101010101100000000000000000000000000000*2^-2
d = 1.0101010101010101010101010101010101010101010101010101*2^-2
The output also shows that a single-precision number is promoted to double-precision by adding zeros in the binary representation.
References and Further Reading¶
The reference for the IEEE standard is,
- ANSI/IEEE Std 754-1985, IEEE Standard for Binary Floating-Point Arithmetic.
A more pedagogical introduction to the standard can be found in the following paper,
- David Goldberg: What Every Computer Scientist Should Know About Floating-Point Arithmetic. ACM Computing Surveys, Vol.: 23, No.: 1 (March 1991), pages 5–48.
- Corrigendum: ACM Computing Surveys, Vol.: 23, No.: 3 (September 1991), page 413. and see also the sections by B. A. Wichmann and Charles B. Dunham in Surveyor’s Forum: “What Every Computer Scientist Should Know About Floating-Point Arithmetic”. ACM Computing Surveys, Vol.: 24, No.: 3 (September 1992), page 319.
A detailed textbook on IEEE arithmetic and its practical use is available from SIAM Press,
- Michael L. Overton, Numerical Computing with IEEE Floating Point Arithmetic, SIAM Press, ISBN 0898715717.