Mathematical Functions¶
This chapter describes basic mathematical functions. Some of these functions are present in system libraries, but the alternative versions given here can be used as a substitute when the system functions are not available.
The functions and macros described in this chapter are defined in the
header file cml/math.h.
Mathematical Constants¶
The library ensures that the standard BSD mathematical constants are defined. For reference, here is a list of the constants:
M_E |
The base of exponentials,  |
M_LOG2E |
The base-2 logarithm of  , , 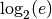 |
M_LOG10E |
The base-10 logarithm of  , , 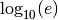 |
M_SQRT2 |
The square root of two, 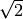 |
M_SQRT1_2 |
The square root of one-half,  |
M_SQRT3 |
The square root of three, 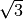 |
M_PI |
The constant pi, 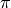 |
M_PI_2 |
Pi divided by two, 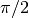 |
M_PI_4 |
Pi divided by four, 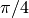 |
M_SQRTPI |
The square root of pi, 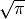 |
M_2_SQRTPI |
Two divided by the square root of pi, 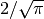 |
M_1_PI |
The reciprocal of pi, 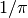 |
M_2_PI |
Twice the reciprocal of pi, 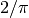 |
M_LN10 |
The natural logarithm of ten,  |
M_LN2 |
The natural logarithm of two, 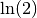 |
M_LNPI |
The natural logarithm of pi, 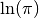 |
M_EULER |
Euler’s constant, 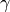 |
Infinities and Not-a-number¶
-
POSINF¶ This macro contains the IEEE representation of positive infinity,
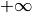 . It is computed from the expression
. It is computed from the expression +1.0/0.0.
-
NEGINF¶ This macro contains the IEEE representation of negative infinity,
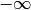 . It is computed from the expression
. It is computed from the expression -1.0/0.0.
-
NAN¶ This macro contains the IEEE representation of the Not-a-Number symbol,
NaN. It is computed from the ratio0.0/0.0.
-
bool
cml_isnan(double x)¶ This function returns 1 if
xis not-a-number.
-
bool
cml_isinf(double x)¶ This function returns
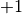 if
if xis positive infinity, if
if xis negative infinity and 0 otherwise. [1]
-
bool
cml_isfinite(double x)¶ This function returns 1 if
xis a real number, and 0 if it is infinite or not-a-number.
Elementary Functions¶
The following routines provide portable implementations of functions
found in the BSD math library. When native versions are not available
the functions described here can be used instead. The substitution can
be made automatically if you use autoconf to compile your
application (see portability-functions).
-
double
cml_log1p(double x)¶ This function computes the value of
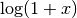 in a way that is
accurate for small
in a way that is
accurate for small x. It provides an alternative to the BSD math functionlog1p(x).
-
double
cml_expm1(double x)¶ This function computes the value of
 in a way that is
accurate for small
in a way that is
accurate for small x. It provides an alternative to the BSD math functionexpm1(x).
-
double
cml_hypot(double x, double y)¶ This function computes the value of
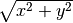 in a way that avoids overflow. It provides an
alternative to the BSD math function
in a way that avoids overflow. It provides an
alternative to the BSD math function hypot(x,y).
-
double
cml_hypot3(double x, double y, double cml_z)¶ This function computes the value of
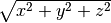 in a way that avoids overflow.
in a way that avoids overflow.
-
double
cml_acosh(double x)¶ This function computes the value of
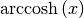 . It provides an
alternative to the standard math function
. It provides an
alternative to the standard math function acosh(x).
-
double
cml_asinh(double x)¶ This function computes the value of
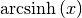 . It provides an
alternative to the standard math function
. It provides an
alternative to the standard math function asinh(x).
-
double
cml_atanh(double x)¶ This function computes the value of
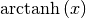 . It provides an
alternative to the standard math function
. It provides an
alternative to the standard math function atanh(x).
-
double
cml_ldexp(double x, int e)¶ This function computes the value of
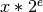 . It provides an
alternative to the standard math function
. It provides an
alternative to the standard math function ldexp(x,e).
-
double
cml_frexp(double x, int *e)¶ This function splits the number
xinto its normalized fraction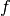 and exponent
and exponent  , such that
, such that 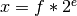 and
and
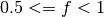 . The function returns
. The function returns 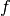 and stores the
exponent in
and stores the
exponent in  . If
. If 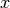 is zero, both
is zero, both 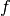 and
and  are set to zero. This function provides an alternative to the standard
math function
are set to zero. This function provides an alternative to the standard
math function frexp(x, e).
Small integer powers¶
A common complaint about the standard C library is its lack of a function for calculating (small) integer powers. CML provides some simple functions to fill this gap. For reasons of efficiency, these functions do not check for overflow or underflow conditions.
-
double
cml_pow_int(double x, int n)¶ -
double
cml_pow_uint(double x, unsigned int n)¶ These routines computes the power
 for integer
for integer n. The power is computed efficiently—for example,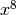 is computed as
is computed as
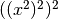 , requiring only 3 multiplications.
, requiring only 3 multiplications.
-
double
cml_pow_2(double x)¶ -
double
cml_pow_3(double x)¶ -
double
cml_pow_4(double x)¶ -
double
cml_pow_5(double x)¶ -
double
cml_pow_6(double x)¶ -
double
cml_pow_7(double x)¶ -
double
cml_pow_8(double x)¶ -
double
cml_pow_9(double x)¶ These functions can be used to compute small integer powers
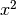 ,
,
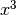 , etc. efficiently. The functions will be inlined when
, etc. efficiently. The functions will be inlined when
HAVE_INLINEis defined, so that use of these functions should be as efficient as explicitly writing the corresponding product expression:#include <cml.h> [...] double y = pow_4(3.141); /* compute 3.141**4 */
Testing the Sign of Numbers¶
-
double
cml_sgn(double x)¶ This macro returns the sign of
x. It is defined as((x) >= 0 ? 1 : -1). Note that with this definition the sign of zero is positive (regardless of its IEEE sign bit).
Maximum and Minimum functions¶
Note that the following macros perform multiple evaluations of their arguments, so they should not be used with arguments that have side effects (such as a call to a random number generator).
-
CML_MAX(a, b)¶ This macro returns the maximum of
aandb. It is defined as((a) > (b) ? (a):(b)).
-
CML_MIN(a, b)¶ This macro returns the minimum of
aandb. It is defined as((a) < (b) ? (a):(b)).
Approximate Comparison of Floating Point Numbers¶
It is sometimes useful to be able to compare two floating point numbers approximately, to allow for rounding and truncation errors. The following function implements the approximate floating-point comparison algorithm proposed by D.E. Knuth in Section 4.2.2 of “Seminumerical Algorithms” (3rd edition).
-
bool
cml_cmp(double x, double y, double epsilon)¶ This function determines whether
xandyare approximately equal to a relative accuracyepsilon.The relative accuracy is measured using an interval of size
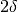 , where
, where 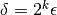 and
and 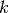 is the
maximum base-2 exponent of
is the
maximum base-2 exponent of 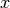 and
and 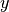 as computed by the
function
as computed by the
function frexp().If
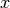 and
and 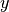 lie within this interval, they are considered
approximately equal and the function returns 0. Otherwise if
lie within this interval, they are considered
approximately equal and the function returns 0. Otherwise if 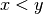 , the function returns
, the function returns  , or if
, or if 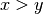 , the function returns
, the function returns
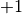 .
.Note that
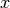 and
and 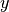 are compared to relative accuracy, so
this function is not suitable for testing whether a value is
approximately zero.
are compared to relative accuracy, so
this function is not suitable for testing whether a value is
approximately zero.The implementation is based on the package
fcmpby T.C. Belding.
Footnotes
| [1] | Note that the C99 standard only requires the
system isinf() function to return a non-zero value, without the
sign of the infinity. The implementation in some earlier versions of
CML used the system isinf() function and may have this behavior
on some platforms. Therefore, it is advisable to test the sign of
x separately, if needed, rather than relying the sign of the
return value from isinf(). |